 login/create account
login/create account
Conjecture The poset of completary multifuncoids of the form 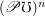 is for every sets
is for every sets 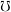 and
and  :
:
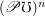 is for every sets
is for every sets 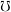 and
and  :
:- \item atomic; \item atomistic.
See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Definition Let 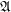 is a family of join-semilattice. A completary multifuncoid of the form
is a family of join-semilattice. A completary multifuncoid of the form 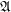 is an
is an 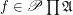 such that we have that:
such that we have that:
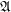 is a family of join-semilattice. A completary multifuncoid of the form
is a family of join-semilattice. A completary multifuncoid of the form 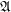 is an
is an 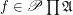 such that we have that:
such that we have that:- \item
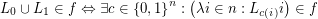 for every
for every 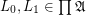 .
.
\item If 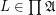 and
and 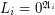 for some
for some  then
then  .
.
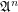 is a function space over a poset
is a function space over a poset 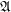 that is
that is 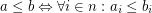 for
for 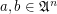 .
.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University