 login/create account
login/create account
Schönheim, J.
Combinatorial covering designs ★
Author(s): Gordon; Mills; Rödl; Schönheim
A 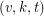 covering design, or covering, is a family of
covering design, or covering, is a family of  -subsets, called blocks, chosen from a
-subsets, called blocks, chosen from a  -set, such that each
-set, such that each  -subset is contained in at least one of the blocks. The number of blocks is the covering’s size, and the minimum size of such a covering is denoted by
-subset is contained in at least one of the blocks. The number of blocks is the covering’s size, and the minimum size of such a covering is denoted by 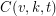 .
.
Problem Find a closed form, recurrence, or better bounds for 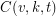 . Find a procedure for constructing minimal coverings.
. Find a procedure for constructing minimal coverings.
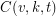 . Find a procedure for constructing minimal coverings.
. Find a procedure for constructing minimal coverings. Keywords: recreational mathematics

 Drupal
Drupal CSI of Charles University
CSI of Charles University