Home » Subject » Combinatorics » Designs
Importance: Low ✭
Author(s): Gordon, D.M.
Mills, W.H.
Rödl, V.
Schönheim, J.
Subject: Combinatorics
» Designs
Keywords: recreational mathematics
Recomm. for undergrads: no
Posted by: Pseudonym
on: April 11th, 2008

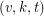A $ (v, k, t) $ covering design, or covering, is a family of $ k $-subsets, called blocks, chosen from a $ v $-set, such that each $ t $-subset is contained in at least one of the blocks. The number of blocks is the covering’s size, and the minimum size of such a covering is denoted by $ C(v, k, t) $.

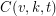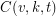Problem   Find a closed form, recurrence, or better bounds for $ C(v,k,t) $. Find a procedure for constructing minimal coverings.

The problem has applications in file design, but is also known at the "lottery cover problem", for its strategic application in playing lotteries.

Current "best" covers have been collected by Dan Gordon.

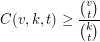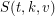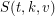The trivial lower bound is $ C(v,k,t) \geq \dfrac{\binom{v}{t}}{\binom{k}{t}} $. When equality holds, the resulting design is called a Steiner system, and often denoted $ S(t,k,v) $. If $ S(t,k,v) $ exists, so does 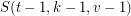$ S(t-1,k-1,v-1) $: just remove all occurrences of a point from the blocks containing it, and discard the blocks that didn't contain it before the deletion.

Bibliography

J. Schönheim, On coverings, Pacific Journal of Mathematics, 14:1405–1411, 1964.

Daniel M. Gordon, Oren Patashnik, Greg Kuperberg (1995) New constructions for covering designs, J. Combinatorial Designs 3(4), 269-284.

D. T. Todorov. Combinatorial Coverings. PhD thesis, University of Sofia, 1985.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options