 login/create account
login/create account
Ramsey number
Ramsey properties of Cayley graphs ★★★
Author(s): Alon
Conjecture There exists a fixed constant  so that every abelian group
so that every abelian group 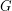 has a subset
has a subset 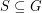 with
with 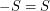 so that the Cayley graph
so that the Cayley graph 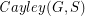 has no clique or independent set of size
has no clique or independent set of size  .
.
 so that every abelian group
so that every abelian group 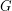 has a subset
has a subset 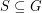 with
with 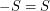 so that the Cayley graph
so that the Cayley graph 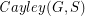 has no clique or independent set of size
has no clique or independent set of size  .
. Keywords: Cayley graph; Ramsey number
Diagonal Ramsey numbers ★★★★
Author(s): Erdos
Let 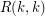 denote the
denote the 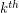 diagonal Ramsey number.
diagonal Ramsey number.
Conjecture 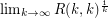 exists.
exists.
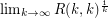 exists.
exists. Problem Determine the limit in the above conjecture (assuming it exists).
Keywords: Ramsey number

 Drupal
Drupal CSI of Charles University
CSI of Charles University