 login/create account
login/create account
Cayley graph
Ramsey properties of Cayley graphs ★★★
Author(s): Alon
Conjecture There exists a fixed constant  so that every abelian group
so that every abelian group  has a subset
has a subset 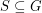 with
with 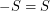 so that the Cayley graph
so that the Cayley graph 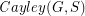 has no clique or independent set of size
has no clique or independent set of size  .
.
 so that every abelian group
so that every abelian group  has a subset
has a subset 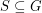 with
with 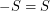 so that the Cayley graph
so that the Cayley graph  has no clique or independent set of size
has no clique or independent set of size  .
. Keywords: Cayley graph; Ramsey number
Cores of Cayley graphs ★★
Author(s): Samal
Conjecture Let  be an abelian group. Is the core of a Cayley graph (on some power of
be an abelian group. Is the core of a Cayley graph (on some power of  ) a Cayley graph (on some power of
) a Cayley graph (on some power of  )?
)?
 be an abelian group. Is the core of a Cayley graph (on some power of
be an abelian group. Is the core of a Cayley graph (on some power of  ) a Cayley graph (on some power of
) a Cayley graph (on some power of  )?
)? Keywords: Cayley graph; core

 Drupal
Drupal CSI of Charles University
CSI of Charles University