 login/create account
login/create account
multidimensional
What are hyperfuncoids isomorphic to? ★★
Author(s): Porton
Let 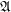 be an indexed family of sets.
be an indexed family of sets.
Products are 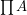 for
for 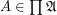 .
.
Hyperfuncoids are filters 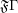 on the lattice
on the lattice 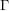 of all finite unions of products.
of all finite unions of products.
Problem Is 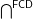 a bijection from hyperfuncoids
a bijection from hyperfuncoids 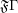 to:
to:
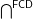 a bijection from hyperfuncoids
a bijection from hyperfuncoids 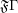 to:
to:- \item prestaroids on
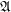 ; \item staroids on
; \item staroids on 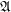 ; \item completary staroids on
; \item completary staroids on 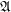 ?
? If yes, is 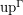 defining the inverse bijection? If not, characterize the image of the function
defining the inverse bijection? If not, characterize the image of the function 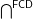 defined on
defined on 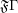 .
.
Consider also the variant of this problem with the set 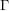 replaced with the set
replaced with the set 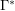 of complements of elements of the set
of complements of elements of the set 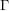 .
.
Keywords: hyperfuncoids; multidimensional

 Drupal
Drupal CSI of Charles University
CSI of Charles University