 login/create account
login/create account
Jain, Kamal
Unit vector flows ★★
Author(s): Jain
Conjecture There exists a map 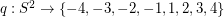 so that antipodal points of
so that antipodal points of 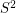 receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero.
receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero.
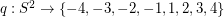 so that antipodal points of
so that antipodal points of 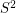 receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero.
receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero. Keywords: nowhere-zero flow

 without a
without a 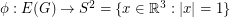 .
.
 Drupal
Drupal CSI of Charles University
CSI of Charles University