 login/create account
login/create account
Unit vector flows
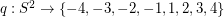 so that antipodal points of
so that antipodal points of 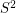 receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero.
receive opposite values, and so that any three points which are equidistant on a great circle have values which sum to zero. The main interest in these two conjectures is that together they imply Tutte's 5-flow conjecture. This follows easily from the fact that the 5-flow conjecture can be reduced to cubic graphs without bridges, and for such a graph  , the composition of the maps
, the composition of the maps 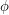 and
and 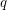 (given by the above conjectures) is a nowhere-zero 5-flow.
(given by the above conjectures) is a nowhere-zero 5-flow.
There are a couple of easy partial results toward the first conjecture which follow from well-known flow/cycle-cover results. First, Tutte showed that every graph with a nowhere-zero 4-flow has a list of three 2-flows 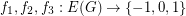 so that every edge is in the support of exactly two of these flows. Combining these flows and normalizing appropriately gives an
so that every edge is in the support of exactly two of these flows. Combining these flows and normalizing appropriately gives an 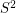 -flow. Bermond, Jackson, and Jaeger [BJJ] showed that every graph with no bridge has a list of seven 2-flows so that every edge is in the support of exactly four of these flows. Combining these and normalizing appropriately gives an
-flow. Bermond, Jackson, and Jaeger [BJJ] showed that every graph with no bridge has a list of seven 2-flows so that every edge is in the support of exactly four of these flows. Combining these and normalizing appropriately gives an 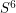 -flow.
-flow.
It seems likely that a graph has an 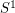 -flow if and only if it has a nowhere-zero 3-flow. The "if" direction of this implication isn't hard to show and the "only if" direction looks quite possible.
-flow if and only if it has a nowhere-zero 3-flow. The "if" direction of this implication isn't hard to show and the "only if" direction looks quite possible.
A dual concept to that of a flow is that of a tension. Observe that a graph  has a
has a 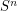 tension if and only if can be embedded in
tension if and only if can be embedded in 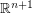 so that all edges are unit length line segments. Such embeddings have received some attention over the years. In particular, there is considerable interest in finding the best possible upper bound on the chromatic number of graphs which embed in
so that all edges are unit length line segments. Such embeddings have received some attention over the years. In particular, there is considerable interest in finding the best possible upper bound on the chromatic number of graphs which embed in 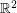 in this manner. This is Hadwinger-Nelson problem on coloring the plane.
in this manner. This is Hadwinger-Nelson problem on coloring the plane.
Bibliography
[BJJ] J.C. Bermond, B. Jackson, and F. Jaeger, Shortest covering of graphs with cycles, J. Combinatorial Theory Ser. B 35 (1983), 297-308. MRhref{0735197}
[T54] W.T. Tutte, A Contribution on the Theory of Chromatic Polynomials, Canad. J. Math. 6 (1954) 80-91. MathSciNet
[T66] W.T. Tutte, On the Algebraic Theory of Graph Colorings, J. Combinatorial Theory 1 (1966) 15-50. MathSciNet
* indicates original appearance(s) of problem.

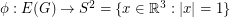 .
.
 Drupal
Drupal CSI of Charles University
CSI of Charles University