 login/create account
login/create account
direct product of filters
Outer reloid of restricted funcoid ★★
Author(s): Porton
Question 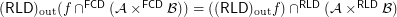 for every filter objects
for every filter objects 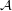 and
and 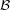 and a funcoid
and a funcoid 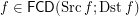 ?
?
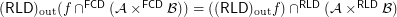 for every filter objects
for every filter objects 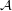 and
and 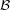 and a funcoid
and a funcoid 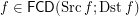 ?
? Keywords: direct product of filters; outer reloid
Outer reloid of direct product of filters ★★
Author(s): Porton
Question 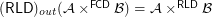 for every f.o.
for every f.o.  ,
,  ?
?
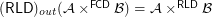 for every f.o.
for every f.o. 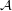 ,
, 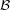 ?
? Keywords: direct product of filters; outer reloid

 Drupal
Drupal CSI of Charles University
CSI of Charles University