 login/create account
login/create account
Upgrading a completary multifuncoid
Let 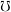 be a set,
be a set, 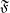 be the set of filters on
be the set of filters on 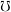 ordered reverse to set-theoretic inclusion,
ordered reverse to set-theoretic inclusion, 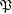 be the set of principal filters on
be the set of principal filters on 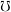 , let
, let  be an index set. Consider the filtrator
be an index set. Consider the filtrator 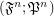 .
.
Conjecture If  is a completary multifuncoid of the form
is a completary multifuncoid of the form 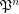 , then
, then 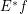 is a completary multifuncoid of the form
is a completary multifuncoid of the form 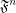 .
.
 is a completary multifuncoid of the form
is a completary multifuncoid of the form 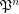 , then
, then 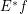 is a completary multifuncoid of the form
is a completary multifuncoid of the form 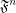 .
. See below for definition of all concepts and symbols used to in this conjecture.
Refer to this Web site for the theory which I now attempt to generalize.
Definition A filtrator is a pair 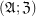 of a poset
of a poset 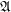 and its subset
and its subset 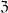 .
.
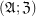 of a poset
of a poset 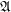 and its subset
and its subset 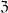 .
. Having fixed a filtrator, we define:
Definition 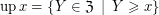 for every
for every 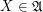 .
.
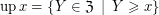 for every
for every 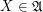 .
. Definition 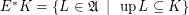 (upgrading the set
(upgrading the set 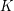 ) for every
) for every 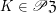 .
.
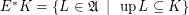 (upgrading the set
(upgrading the set 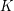 ) for every
) for every 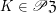 .
. Definition Let 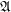 is a family of join-semilattice. A completary multifuncoid of the form
is a family of join-semilattice. A completary multifuncoid of the form 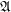 is an
is an 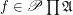 such that we have that:
such that we have that:
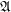 is a family of join-semilattice. A completary multifuncoid of the form
is a family of join-semilattice. A completary multifuncoid of the form 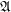 is an
is an 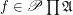 such that we have that:
such that we have that:- \item
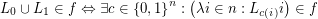 for every
for every 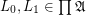 .
.
\item If 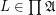 and
and 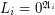 for some
for some  then
then  .
.
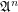 is a function space over a poset
is a function space over a poset 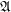 that is
that is 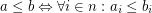 for
for 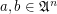 .
.
For finite  this problem is equivalent to Upgrading a multifuncoid .
this problem is equivalent to Upgrading a multifuncoid .
It is not hard to prove this conjecture for the case 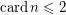 using the techniques from this my article. But I failed to prove it for
using the techniques from this my article. But I failed to prove it for 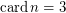 and above.
and above.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University