 login/create account
login/create account
Unconditional derandomization of Arthur-Merlin games
It is trivial to show that 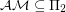 . It is also known that under hardness assumptions
. It is also known that under hardness assumptions 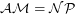 (See [MV99]). The question is, can we prove unconditionally that
(See [MV99]). The question is, can we prove unconditionally that 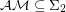 .
.
Bibliography
*[GSTS03] Danny Gutfreund, Ronen Shaltiel and Amnon Ta-Shma, Uniform hardness vs. randomness for Arthur-Merlin games, Proc. of CCC 2003. Can be downloaded from Ronen Shaltiel's web site.
[MV99] Peter Bro Miltersen and N. Variyam Vinodchandran, "Derandomizing Arthur-Merlin games using hitting sets", STOC 1999, pages 71-80. Can be downloaded from N. Variyam Vinodchandran's web site.
[SU01] Ronen Shaltiel and Christopher Umans, Simple extractor for all min-entropies and new pseudo-random generator, Proc. of FOCS 2001, pages 648-657. Can be downloaded from Ronen Shaltiel's web site.
[SU07] Ronen Shaltiel and Christopher Umans, Low-end uniform hardness vs. randomness tradeoffs for AM, STOC 2007. Can be downloaded from Ronen Shaltiel's web site.
* indicates original appearance(s) of problem.

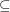
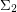
 Drupal
Drupal CSI of Charles University
CSI of Charles University