 login/create account
login/create account
The 3n+1 conjecture
Conjecture Let 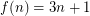 if
if  is odd and
is odd and 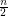 if
if  is even. Let
is even. Let 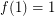 . Assume we start with some number
. Assume we start with some number  and repeatedly take the
and repeatedly take the 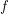 of the current number. Prove that no matter what the initial number is we eventually reach
of the current number. Prove that no matter what the initial number is we eventually reach 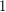 .
.
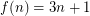 if
if  is odd and
is odd and 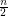 if
if  is even. Let
is even. Let 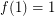 . Assume we start with some number
. Assume we start with some number  and repeatedly take the
and repeatedly take the 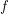 of the current number. Prove that no matter what the initial number is we eventually reach
of the current number. Prove that no matter what the initial number is we eventually reach 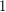 .
. This problem is also called Collatz conjecture, Ulam conjecture, or the Syracuse problem. For a more extensive discussion, visit the wikipedia article or [L].
Bibliography
[L] Jeffrey C. Lagarias: The 3x+1 problem: An annotated bibliography (1963--2000)
* indicates original appearance(s) of problem.
Bruckman proved 3x+1 problem
On April 9th, 2008 porton says:
From PlanetMath's forums:
> Bruckman has published his proof of the conjecture in the International Journal of Mathematical Education in Science and Technology,
> Vol 39, Issue 3 April 2008.
--
Victor Porton - http://www.mathematics21.org
In The 3x+1 Problem: An
On June 11th, 2008 brenton says:
In The 3x+1 Problem: An Annotated Bibliography, II (2001-), Lagarias explains why this proof is incomplete.
Somebody's efforts
On January 14th, 2008 porton says:
At http://occampress.com/ somebody publishes something about 3n+1 problem. Read him and check whether he is true.
Victor Porton - http://www.mathematics21.org

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Peter Schorer, again a possible proof
Just last month, July 2014, Schorer published another paper which uses similar methods as from his 2008 paper, claiming again to have proven the conjecture. This is early, but I am wanting to know what the general opinion of Schorer is in the world of serious mathematicians. All of my research has turned up mixed reviews and heated arguments.