Snevily's conjecture

Importance: High ✭✭✭

Author(s):

Subject:	Number Theory
	» Combinatorial Number Theory

Keywords:	addition table
	latin square
	transversal

Recomm. for undergrads: yes

Posted	by:	mdevos
	on:	October 13th, 2007

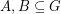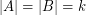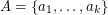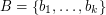Conjecture Let $G$ be an abelian group of odd order and let $A,B \subseteq G$ satisfy $|A| = |B| = k$ . Then the elements of $A$ and $B$ may be ordered $A = \{a_1,\ldots,a_k\}$ and $B = \{b_1,\ldots,b_k\}$ so that the sums 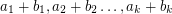$a_1+b_1, a_2+b_2 \ldots, a_k + b_k$ are pairwise distinct.

The motivation for this question comes from the study of latin squares. The addition table of every (additive) group forms a latin square, and this gives us a rich source of interesting squares. To explain further, we require a couple of definitions. A transversal of a 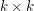$k \times k$ matrix is a collection of $k$ cells, no two of which are in the same row or column, and we say that a transversal is latin if no two of its cells contain the same element. Latin transversals are nice structures to find in latin squares. 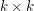In particular, note that the cells of a $k \times k$ latin square $L$ may be partitioned into $k$ latin transversals if and only if there is a latin square orthogonal to $L$ (see this for a definition of orthogonal latin squares). The above conjecture is perhaps most naturally phrased in terms of latin transversals as follows.

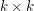Conjecture (Snevily's conjecture - version 2) Every $k \times k$ submatrix of the addition table of every abelian group of odd order has a latin transversal.

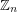Snevily's conjecture was proved by Alon [A] for abelian groups of prime order using a fairly standard application of the Alon-Tarsi polynomial technique. 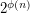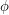Later, Dasgupta, Karolyi, Serra, and Szegedy [DKSSz] used a sneaky application of the same technique to prove the conjecture for cyclic groups of odd order (the key to their approach is the fact that for $n$ odd, ${\mathbb Z}_n$ is a subgroup of the multiplicative group of the field of order $2^{\phi(n)}$ where $\phi$ is Euler's totient function). The conjecture is still open for non-cyclic groups.

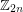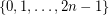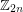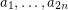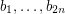The full addition table of ${\mathbb Z}_{2n}$ does not have a latin transversal. To see this, note that the sum of the elements in this group is equal to $n$ (here we identify $\{0,1,\ldots,2n-1\}$ with ${\mathbb Z}_{2n}$ in the usual manner). So, if $a_1,\ldots,a_{2n}$ and $b_1,\ldots,b_{2n}$ are two orderings of 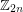${\mathbb Z}_{2n}$ , then 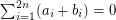$\sum_{i=1}^{2n} (a_i + b_i) = 0$ , and therefore 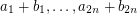$a_1 + b_1,\ldots,a_{2n} + b_{2n}$ cannot be an ordering of 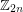${\mathbb Z}_{2n}$ . This parity problem is the only obstruction known, and the following conjecture asserts that apart from it, the above conjectures holds for cyclic groups of even order.

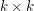Conjecture (Snevily) Every $k \times k$ submatrix of the addition table of 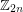${\mathbb Z}_{2n}$ has a latin transversal, unless it is a translate of a cyclic subgroup of 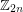${\mathbb Z}_{2n}$ of even order.

In fact, it appears that the above conjecture might hold with 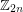${\mathbb Z}_{2n}$ replaced by any abelian group.

Bibliography

[A] N. Alon, Additive Latin transversals. Israel J. Math. 117 (2000), 125--130. MathSciNet

[DKSSz] S. Dasgupta, Gy. Károlyi, O. Serra, B. Szegedy, Transversals of additive Latin squares. Israel J. Math. 126 (2001), 17--28. MathSciNet

*[S] H. S. Snevily, Unsolved Problems: The Cayley Addition Table of Z $\sb n$ . Amer. Math. Monthly 106 (1999), no. 6, 584--585. MathSciNet.

* indicates original appearance(s) of problem.

add new comment

Proof of Snevily's Conjecture

On May 27th, 2011 G. Eric Moorhouse says:

Snevily's Conjecture was in fact proved in 2009. See: Bodan Arsovski, 'A proof of Snevily's Conjecture', Israel Journal of Mathematics, vol. 182 (2011), pp. 505-508. See also Gergely Harcos, Gyula Károlyi and Géza Kós, 'Remarks to Arsovski's proof of Snevily's Conjecture', Annales Univ. Sci. Budapest., vol. 54 (2011), pp. 57-61.

Open Problem Garden

Snevily's conjecture

Bibliography

Proof of Snevily's Conjecture

Comment viewing options

Navigate

Recent Activity