Home » Subject » Number Theory » Combinatorial N.T.

Sets with distinct subset sums

Importance: High ✭✭✭
Author(s): Erdos, Paul
Subject: Number Theory
» Combinatorial Number Theory
Keywords: subset sum
Recomm. for undergrads: no
Prize: $500 (Erdos-Graham)
Posted by: mdevos
on: June 24th, 2007

Say that a set 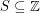$ S \subseteq {\mathbb Z} $ has distinct subset sums if distinct subsets of $ S $ have distinct sums.

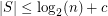Conjecture   There exists a fixed constant $ c $ so that $ |S| \le \log_2(n) + c $ whenever 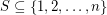$ S \subseteq \{1,2,\ldots,n\} $ has distinct subset sums.

Erdos valued this problem at $500, and I (M. DeVos) believe these prizes are now supported by Ron Graham.

Define the function 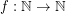$ f : {\mathbb N} \rightarrow {\mathbb N} $ by the rule \[ f(n) = \min \{ \max S : S \subseteq {\mathbb N} \mbox{ has distinct subset sums and } |S| = n \} \]

Then Erdos' conjecture is equivalent to the assertion that 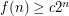$ f(n) \ge c 2^n $ for a fixed constant $ c $, and more generally, we would like to understand the behavior of $ f $.

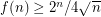Erdos and Moser established an upper bound on $ f $, proving that $ f(n) \ge 2^n / 4 \sqrt{n} $. This was later improved by a constant factor by Elkies [E].

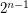We get an easy lower bound on $ f $ by observing that the set $ S $ consisting of the first $ n $ powers of 2 has distinct subset sums, and has maximal element $ 2^{n-1} $. This shows that 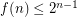$ f(n) \le 2^{n-1} $. At first glance, it might appear that such sets are optimal, but these sets have too many small numbers, and it is possible to improve upon them. Conway and Guy [CG] found a construction of sets with distinct subset sum, now called the Conway-Guy sequence, which gives an interesting upper bound on $ f $. This was this was later improved by Lunnan [L], and then by Bohman [B] to 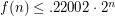$ f(n) \le .22002 \cdot 2^n $ (for $ n $ sufficiently large).

Bibliography

[B] T. Bohman, A construction for sets of integers with distinct subset sums, The Electronic. Journal of Combinatorics 5 (1998) /#R3

[CG] J. H. Conway and R. K. Guy, Sets of natural numbers with distinct subset sums, Notices, Amer. Math. Soc., 15 (1968) 345.

[E] N. Elkies, An improved lower bound on the greatest element of a sum-distinct set of fixed order, J. Comb. Th. A, 41 (1986) 89-94.

[G1] R. K. Guy, Sets of integers whose subsets have distinct sums, Ann. Discrete Math., 12 (1982) 141-154.

[G2] R. K. Guy, Unsolved Problems in Number Theory, Springer-Verlag, 1981.

[L] W. F. Lunnon, Integers sets with distinct subset sums, Math. Compute, 50 (1988) 297-320.


* indicates original appearance(s) of problem.
add new comment

Mistake

On April 7th, 2011 Anonymous says:

You are referring to the first upper bound as a lower bound, and the lower bound as an upper bound.

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.