 login/create account
login/create account
Primitive pythagorean n-tuple tree
Conjecture Find linear transformation construction of primitive pythagorean n-tuple tree!
Primitive pythagorean n-tuple is a n-tuple 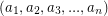 such that
such that 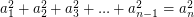
and the greatest common divisor of 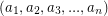 is 1.
is 1.
Is there any other linear transformation construction of primitive pythagorean triple tree?
Moreover, find linear transformation construction of primitive pythagorean n-tuple tree!
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Linear transformation of primitive pythagorean n-tuple
Is it true that for primitive pythagorean n-tuple (a_1, a_2...... a_n), if there are (n-2) even terms and 1 odd term in the summation side of the equation and a_n is odd, a linear transformation can be made? And can we find any such primitive pythagorean n-tuple where a_n is even?