Home » Subject » Graph Theory

Minimum number of arc-disjoint transitive subtournaments of order 3 in a tournament

Importance: Medium ✭✭
Author(s): Yuster, Raphael
Subject: Graph Theory
Keywords:
Recomm. for undergrads: no
Posted by: fhavet
on: May 21st, 2013
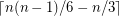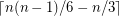Conjecture   If $ T $ is a tournament of order $ n $, then it contains $ \left \lceil n(n-1)/6 - n/3\right\rceil $ arc-disjoint transitive subtournaments of order 3.

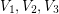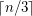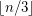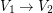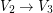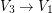If true the conjecture would be tight as shown by any tournament whose vertex set can be decomposed into $ 3 $ sets $ V_1, V_2, V_3 $ of size $ \lceil n/3 \rceil $ or $ \lfloor n/3\rfloor $ and such that $ V_1\rightarrow V_2 $, $ V_2\rightarrow V_3 $ and $ V_3\rightarrow V_1 $.

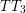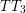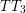Let $ TT_3 $ denote the transitive tournament of order 3. A $ TT_3 $-packing of a digraph $ D $ is a set of arc-disjoint copies of $ TT_3 $ subgraphs of $ D $.

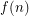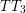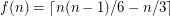Let $ f(n) $ be the minimum size of a $ TT_3 $-packing over all tournaments of order $ n $. The conjecture and its tightness say $ f(n)= \left \lceil n(n-1)/6 - n/3\right\rceil $.

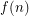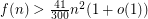The best lower bound for $ f(n) $ so far is due to Kabiya and Yuster [KY] proved that $ f(n) > \frac{41}{300} n^2(1+o(1)) $.

Bibliography

[KY] M. Kabiya and R. Yuster. Packing transitive triples in a tournament. Ann. Comb. 12 (2008), no. 3, 291–-306.

*[Y] R. Yuster. The number of edge-disjoint transitive triples in a tournament. Discrete Math. 287 (2004). no. 1-3,187--191.


* indicates original appearance(s) of problem.
add new comment