 login/create account
login/create account
Length of surreal product
Conjecture Every surreal number has a unique sign expansion, i.e. function 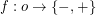 , where
, where  is some ordinal. This
is some ordinal. This  is the length of given sign expansion and also the birthday of the corresponding surreal number. Let us denote this length of
is the length of given sign expansion and also the birthday of the corresponding surreal number. Let us denote this length of  as
as 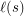 .
.
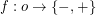 , where
, where  is some ordinal. This
is some ordinal. This  is the length of given sign expansion and also the birthday of the corresponding surreal number. Let us denote this length of
is the length of given sign expansion and also the birthday of the corresponding surreal number. Let us denote this length of  as
as 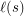 .
.
It is easy to prove that
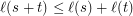
What about
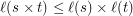
?
This is strongly conjectured to be true by Gonshor in [Gon86]. There is an easy way to prove that
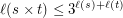
Bibliography
*[Gon86] Harry Gonshor, An Introduction to the Theory of Surreal Numbers, Cambridge University Press, Cambridge, 1986.
* indicates original appearance(s) of problem.
Maybe!
On June 5th, 2012 Lukáš Lánský says:
Thank you! I wasn't aware of this paper. At first sight I think that the part you refer to establish the required result just for surreals in the form 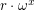 , but I'll find time to go through it thoroughly as it is most relevant for the matter.
, but I'll find time to go through it thoroughly as it is most relevant for the matter.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Proof Already Exists?
I believe the proof for the conjectured statement was proven in the affirmative in the paper "Fields of Surreal Numbers and Exponentiation" by Dries and Ehrlich. Specifically, Lemma 3.3 on page 6 : http://www.ohio.edu/people/ehrlich/EhrlichvandenDries.pdf
If this satisfies the conjecture adequately great, if not, let me know if you would like to work toward a solution together on something similar or related.
Thanks.
-Vincent Russo