 login/create account
login/create account
Large acyclic induced subdigraph in a planar oriented graph.
Conjecture Every planar oriented graph  has an acyclic induced subdigraph of order at least
has an acyclic induced subdigraph of order at least 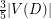 .
.
 has an acyclic induced subdigraph of order at least
has an acyclic induced subdigraph of order at least 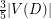 .
. Borodin's 5-Colour Theorem states that every planar graph has an acyclic 5-colouring This implies that every planar oriented graph  has an acyclic induced subdigraph of order at least
has an acyclic induced subdigraph of order at least 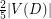 .
.
Already improving this bound to 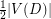 would be interesting: it is a relaxtion of both a Conjecture of Albertson and Berman stating that every planar graph
would be interesting: it is a relaxtion of both a Conjecture of Albertson and Berman stating that every planar graph  has an induced forest of order
has an induced forest of order 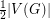 and a Conjecture of Neumann-Lara stating that every planar oriented graph can be split into two acyclic subdigraphs.
and a Conjecture of Neumann-Lara stating that every planar oriented graph can be split into two acyclic subdigraphs.
If true, this conjecture would be best possible.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University