 login/create account
login/create account
Jacobian Conjecture
Conjecture Let  be a field of characteristic zero. A collection
be a field of characteristic zero. A collection 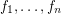 of polynomials in variables
of polynomials in variables 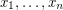 defines an automorphism of
defines an automorphism of 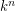 if and only if the Jacobian matrix is a nonzero constant.
if and only if the Jacobian matrix is a nonzero constant.
 be a field of characteristic zero. A collection
be a field of characteristic zero. A collection 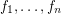 of polynomials in variables
of polynomials in variables 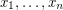 defines an automorphism of
defines an automorphism of 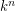 if and only if the Jacobian matrix is a nonzero constant.
if and only if the Jacobian matrix is a nonzero constant. The Jacobian determinant is the determinant of the matrix  with
with 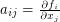 . It is elementary to show that if the map
. It is elementary to show that if the map 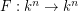 is an automorphism, then the Jacobian determinant is a nonzero constant, by using the inverse map. The other direction has turned out to be rather difficult.
is an automorphism, then the Jacobian determinant is a nonzero constant, by using the inverse map. The other direction has turned out to be rather difficult.
It is known that the Conjecture holds for polynomials of degree 2, and that the general case follows from a special case in degree 3.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Problem statement
iff the determinant of the Jacobian matrix is a nonzero constant.