 login/create account
login/create account
Frobenius number of four or more integers
For 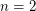 , the formula
, the formula 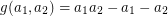 was discovered by Sylvester discovered in 1884 [S]. For
was discovered by Sylvester discovered in 1884 [S]. For 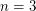 , an explicit solution is also known [G,R,SB]. No explicit solution is known for
, an explicit solution is also known [G,R,SB]. No explicit solution is known for 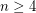 .
.
Bibliography
[G] Greenberg, H. "Solution to a Linear Diophantine Equation for Nonnegative Integers." J. Algorithms 9, 343-353, 1988.
[R] Rødseth, Ø. J. "On a Linear Diophantine Problem of Frobenius." J. reine angew. Math. 301, 171-178, 1978.
[SB] Selmer, E. S. and Beyer, Ö. "On the Linear Diophantine Problem of Frobenius in Three Variables." J. reine angew. Math. 301, 161-170, 1978.
[S] Sylvester, J. J. "Question 7382." Mathematical Questions from the Educational Times 41, 21, 1884.
* indicates original appearance(s) of problem.

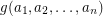 of co-prime positive integers
of co-prime positive integers 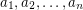 for
for  Drupal
Drupal CSI of Charles University
CSI of Charles University