 login/create account
login/create account
Wall-Sun-Sun primes and Fibonacci divisibility
Conjecture For any prime  , there exists a Fibonacci number divisible by
, there exists a Fibonacci number divisible by  exactly once.
exactly once.
 , there exists a Fibonacci number divisible by
, there exists a Fibonacci number divisible by  exactly once.
exactly once. Equivalently:
Conjecture For any prime 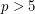 ,
, 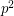 does not divide
does not divide 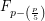 where
where 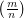 is the Legendre symbol.
is the Legendre symbol.
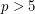 ,
, 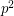 does not divide
does not divide 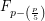 where
where 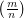 is the Legendre symbol.
is the Legendre symbol.
Let  be an odd prime, and let
be an odd prime, and let 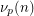 denote the
denote the  -adic valuation of
-adic valuation of  . Let
. Let 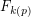 be the smallest Fibonacci number that is divisible by
be the smallest Fibonacci number that is divisible by  (which must exist by a simple counting argument). A well-known result says that
(which must exist by a simple counting argument). A well-known result says that 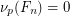 unless
unless 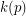 divides
divides  , and
, and 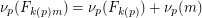 . This conjecture asserts that
. This conjecture asserts that 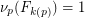 for all
for all  . This has been verified up to at least
. This has been verified up to at least 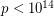 . [EJ]
. [EJ]
This conjecture is equivalent to non-existence of Wall-Sun-Sun primes.
Bibliography
[EJ] Andreas-Stephan Elsenhansand and Jörg Jahnel, The Fibonacci sequence modulo p^2
[R] Marc Renault, Properties of the Fibonacci Sequence Under Various Moduli
*[W] D. D. Wall, Fibonacci Series Modulo m, American Mathematical Monthly, 67 (1960), pp. 525-532.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University