 login/create account
login/create account
F_d versus F_{d+1}
Problem Find a constant  such that for any
such that for any  there is a sequence of tautologies of depth
there is a sequence of tautologies of depth  that have polynomial (or quasi-polynomial) size proofs in depth
that have polynomial (or quasi-polynomial) size proofs in depth 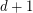 Frege system
Frege system 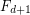 but requires exponential size
but requires exponential size 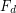 proofs.
proofs.
 such that for any
such that for any  there is a sequence of tautologies of depth
there is a sequence of tautologies of depth  that have polynomial (or quasi-polynomial) size proofs in depth
that have polynomial (or quasi-polynomial) size proofs in depth 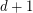 Frege system
Frege system 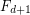 but requires exponential size
but requires exponential size 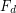 proofs.
proofs. Problem statement from link.
Such tautologies are known if  may depend on
may depend on  (for
(for 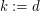 ). This problem is also closely related to conservativity relations among bounded arithmetic theories.
). This problem is also closely related to conservativity relations among bounded arithmetic theories.
Bibliography
*[K1] J.Krajicek: "Lower Bounds to the Size of Constant-Depth Propositional Proofs", J. of Symbolic Logic, 59(1), (1994), pp.73-86
[K2] J. Krajicek: "Bounded arithmetic, propositional logic, and complexity theory", Encyclopedia of Mathematics and Its Applications, Vol.60, Cambridge University Press, Cambridge - New York - Melbourne, (1995), 343 p. (on page 243)
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University