Home » Subject » Algebra

Elementary symmetric of a sum of matrices

Importance: High ✭✭✭
Author(s):
Subject: Algebra
Keywords:
Recomm. for undergrads: no
Posted by: rscosa
on: December 8th, 2008
Problem  

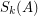Given a Matrix $ A $, the $ k $-th elementary symmetric function of $ A $, namely $ S_k(A) $, is defined as the sum of all $ k $-by-$ k $ principal minors.

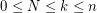Find a closed expression for the $ k $-th elementary symmetric function of a sum of N $ n $-by-$ n $ matrices, with $ 0\le N\le k\le n $ by using partitions.

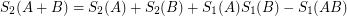The Newton-Girard formulas imply particular expressions for small values of $ k $ and $ N $, for example, $ S_2(A+B)=S_2(A)+S_2(B)+S_1(A)S_1(B)-S_1(AB) $.

Bibliography



* indicates original appearance(s) of problem.
add new comment

that's ok

On August 27th, 2010 olivier says:

that's ok

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.