login/create account
Discrete Logarithm Problem
If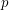 
is prime and 
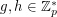, we write 
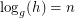if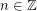 
satisfies 
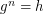. The problem of finding such an integer 
for a given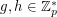 
(with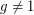 
) is the Discrete Log Problem.
Conjecture There does not exist a polynomial time algorithm to solve the Discrete Log Problem.
The Discrete Logarithm Problem is a critical problem in number theory, and is similar in many ways to the integer factorization problem. If it were possible to compute discrete logs efficiently, it would be possible to break numerous thought-to-be unbreakable cryptographic schemes. However, although most mathematicians and computer scientists believe that the DLP is unsolvable, this conjecture is difficult to establish, because such a proof would imply that P != NP...which is the most difficult open problem in theoretical computer science.
Avi Wigderson has shown that there is no ``natural proof'' (in the sense of [RR]) that the DLP requires circuits of greater than half-exponential size. The key idea is that a natural proof that the DLP is hard would yield a method for breaking discrete-log-based cryptosystems, and this is a contradiction. Of course, it could still be that DLP is provably hard, but by a proof that is not ``natural.''
Bibliography
[RR] Alexander A. Razborov and Steven Rudich, Natural proofs, Journal of Computer and System Sciences 55 (1997), 24–35.
* indicates original appearance(s) of problem.
N != n
On February 25th, 2013 Anonymous says:
The above paper solves the discrete logarithm in time O(N^3) not O(n^3), two very different things. N being the size of the modulus, n being log_2 of N (the binary length). There are many algorithms that will solve the discrete log problem much faster than this method, brute force search runs at a worst case of O(N), or in other words O(2^n). The provided algorithm in the above paper runs in (2^(3*n)).
A polynomial algorithm
On December 29th, 2009 Anonymous says:
See the paper at http://arxiv1.library.cornell.edu/abs/0912.2269.
Drupal
CSI of Charles University
Discrete Logrithm is polynomial
The discrete logarithm problem is little more than an integer analog to a rotor-code cipher problem. The later is a problem in finding concurrent zeros for two periodic functions where the periodicity of one tracks the value of x and the other the value of y. The value of x being x, x^2, x^3, ... x^n. The value of y being y, y+p, y+2p,..., y+np. These forms of problems are amenable to solution using a multi dimensional difference (recurrence) expression (as is the Elliptic Curve Cryptographic problem which is a direct application of DE over algebraic fields). The Discrete Logarithm problem is solvable by a deterministic polynomial time algorithm in O(n^3). Google a paper titled "Computing a Discrete Logarithm in O(n^3)", which can be found at Cornell's arXiv website. Example code for the algorithm is also provided by the author of that paper.