 login/create account
login/create account
Davenport's constant
For a finite (additive) abelian group  , the Davenport constant of
, the Davenport constant of  , denoted
, denoted 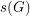 , is the smallest integer
, is the smallest integer  so that every sequence of elements of
so that every sequence of elements of  with length
with length 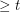 has a nontrivial subsequence which sums to zero.
has a nontrivial subsequence which sums to zero.
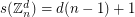
Davenport's original motivation for introducing the constant 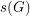 concerned prime ideal decompositions in algebraic number fields. However, determining this constant even for some very restricted families of groups has proved to be an interesting combinatorial problem. Indeed, the highlighted conjecture is considered to be one of the most important unsolved problems concerning finite abelian groups. I (M. DeVos) have reguarded this conjecture as folklore, but I await correction here.
concerned prime ideal decompositions in algebraic number fields. However, determining this constant even for some very restricted families of groups has proved to be an interesting combinatorial problem. Indeed, the highlighted conjecture is considered to be one of the most important unsolved problems concerning finite abelian groups. I (M. DeVos) have reguarded this conjecture as folklore, but I await correction here.
It is easy to see that 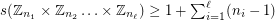 because the sequence constructed by taking
because the sequence constructed by taking  copies of the element with a
copies of the element with a  in the
in the  position and
position and  's elsewhere has no nontrivial subsequence which sums to zero. There is also an easy upper bound of
's elsewhere has no nontrivial subsequence which sums to zero. There is also an easy upper bound of 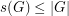 . To see this, assume
. To see this, assume 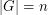 , let
, let 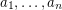 be a sequence of elements from
be a sequence of elements from  , and consider the terms
, and consider the terms 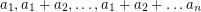 . If these terms are distinct, then one must be 0 (giving us a zero sum subseqence). Otherwise two of them must be equal, so we have
. If these terms are distinct, then one must be 0 (giving us a zero sum subseqence). Otherwise two of them must be equal, so we have 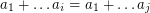 for some
for some 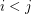 , but then
, but then 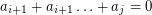 .
.
For cyclic groups, our trivial upper and lower bound match, so we have 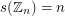 . However, the situation gets much more difficult as soon as we go any further. The following theorem summarizes two classic results of Olson which remain state of the art.
. However, the situation gets much more difficult as soon as we go any further. The following theorem summarizes two classic results of Olson which remain state of the art.
- \item
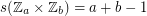 if
if 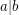 . \item if
. \item if  is prime,
is prime, 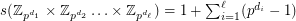
Although there does not even exist a conjecture as to the value of 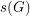 for a general
for a general  , recently a number of authors have proved theorems which give upper bounds on
, recently a number of authors have proved theorems which give upper bounds on 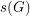 under some structural assumptions. For instance, Caro has proved that
under some structural assumptions. For instance, Caro has proved that 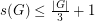 for every
for every  which is not cyclic and not of the form
which is not cyclic and not of the form 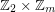 .
.

 Drupal
Drupal CSI of Charles University
CSI of Charles University