 login/create account
login/create account
$C^r$ Stability Conjecture
Conjecture Any 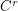 structurally stable diffeomorphism is hyperbolic.
structurally stable diffeomorphism is hyperbolic.
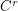 structurally stable diffeomorphism is hyperbolic.
structurally stable diffeomorphism is hyperbolic. See the definitions of: stractural stability and hyperbolicity.
The conjecture is due to J Palis and S Smale (1970's). In the case 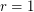 the conjecture was proved by R Mañé (Publ. IHES 1986). In higher regularity,
the conjecture was proved by R Mañé (Publ. IHES 1986). In higher regularity, 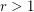 , the conjecture is one of the most important and difficult problems in dynamical systems.
, the conjecture is one of the most important and difficult problems in dynamical systems.
There is a similar conjecture for the vector fields or flows, and in the  topology has been proved by S Hayashi (Ann Math. 1997).
topology has been proved by S Hayashi (Ann Math. 1997).
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University