 login/create account
login/create account
Burnside problem
 generators and exponent
generators and exponent  , is it necessarily finite?
, is it necessarily finite? It is possible to define the 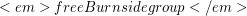
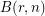 to be the group generated by
to be the group generated by 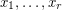 with relations
with relations 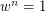 where
where  ranges over every word in the generators. There is a universality property: Any homomorphism
ranges over every word in the generators. There is a universality property: Any homomorphism 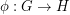 where
where  has r generators and exponent dividing
has r generators and exponent dividing  can be written as a composition of a homomorphism
can be written as a composition of a homomorphism 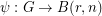 with a homomorphism
with a homomorphism 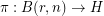 . Some cases of this are known:
. Some cases of this are known: 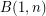 is a cyclic group of order
is a cyclic group of order  , for any positive integer
, for any positive integer  .
. 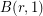 is trivial for any positive integer
is trivial for any positive integer  .
. 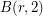 is isomorphic to the Cartesian product of
is isomorphic to the Cartesian product of  cyclic groups of order
cyclic groups of order  , for any positive integer
, for any positive integer  . This is because the relations make it easy to prove that the generators commute.
. This is because the relations make it easy to prove that the generators commute. 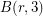 is a finite group, and its order is
is a finite group, and its order is ![\[ 3^{r + \binom{r}{2} + \binom{r}{3}}. \]](/files/tex/cefeed3e688cfea6164da0d2fca76673a63c8a23.png)
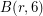 is a finite group, and its order is
is a finite group, and its order is ![\[ 2^{1 + (r-1)3^{r + \binom{r}{2} + \binom{r}{3}} }3^{1 + (r-1)2^{r + \binom{r}{2} + \binom{r}{3}} }. \]](/files/tex/a7d34f67c35a94f0013fefadaddcc401427a5645.png)
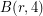 is a finite group for any positive integer
is a finite group for any positive integer  . The order is known for
. The order is known for  up to
up to  :
: ![\[ |B(1,4)| = 2^{2} \]](/files/tex/9314dd52fe1ea1e5e2212e6082c68e873c55e9d3.png)
![\[ |B(2,4)| = 2^{12} \]](/files/tex/e849665500fb42c147d095cc903da0c3ebb8f8b7.png)
![\[ |B(3,4)| = 2^{69} \]](/files/tex/d02ae4aa0f36b9d529ecefb32f7498fc7342c306.png)
![\[ |B(4,4)| = 2^{422} \]](/files/tex/c6b2d4a19596705ac3b303ccdf80ed14f7406a10.png)
![\[ |B(5,4)| = 2^{2728} \]](/files/tex/a6fd794fb98580c4be7c6ebb811ba241d0563e41.png)
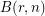 is known to be infinite for sufficiently large
is known to be infinite for sufficiently large  and odd
and odd 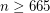 , as well as
, as well as 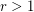 and
and 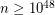 divisible by
divisible by 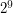 .
.
Bibliography
* indicates original appearance(s) of problem.

![\[</p>
<p>\]](/files/tex/293d7d12d8e7ea226caea2427ba9985877f3ab0c.png)
 Drupal
Drupal CSI of Charles University
CSI of Charles University