 login/create account
login/create account
Book Thickness of Subdivisions
Let  be a finite undirected simple graph.
be a finite undirected simple graph.
A  -page book embedding of
-page book embedding of  consists of a linear order
consists of a linear order 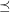 of
of 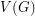 and a (non-proper)
and a (non-proper)  -colouring of
-colouring of 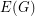 such that edges with the same colour do not cross with respect to
such that edges with the same colour do not cross with respect to 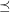 . That is, if
. That is, if 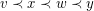 for some edges
for some edges 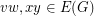 , then
, then  and
and 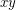 receive distinct colours.
receive distinct colours.
One can think that the vertices are placed along the spine of a book, and the edges are drawn without crossings on the pages of the book.
The book thickness of  , denoted by bt
, denoted by bt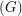 is the minimum integer
is the minimum integer  for which there is a
for which there is a  -page book embedding of
-page book embedding of  .
.
Let 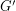 be the graph obtained by subdividing each edge of
be the graph obtained by subdividing each edge of  exactly once.
exactly once.
 such that for every graph
such that for every graph  ,
, 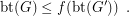
The conjecture is due to [B099]. The conjecture is true for complete graphs [BO99,EM99,E02]. The conjecture is discussed in depth in [DW05].
Bibliography
*[BO99] Robin Blankenship and Bogdan Oporowski. Drawing Subdivisions Of Complete And Complete Bipartite Graphs On Books, Technical Report 1999-4, Department of Mathematics, Louisiana State University, 1999.
[DW05] Vida Dujmovic and David Wood. Stacks, queues and tracks: Layouts of graph subdivisions. Discrete Mathematics & Theoretical Computer Science 7:155-202, 2005.
[EM99] Hikoe Enomoto and Miki Shimabara Miyauchi. Embedding graphs into a three page book with 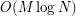 crossings of edges over the spine. SIAM J. Discrete Math., 12(3):337–341, 1999.
crossings of edges over the spine. SIAM J. Discrete Math., 12(3):337–341, 1999.
[E02] David Eppstein. Separating thickness from geometric thickness. In Proc. 10th International Symp. on Graph Drawing (GD ’02), pp. 150–161. vol. 2528 of Lecture Notes in Comput. Sci. Springer, 2002.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
This problem is solved
This problem is solved in:
V. Dujmović, D. Eppstein, R. Hickingbotham, P. Morin, D. R. Wood. Stack-number is not bounded by queue-number. Combinatorica, accepted in 2021 https://arxiv.org/abs/2011.04195