login/create account
Transversal achievement game on a square grid
Problem Two players alternately write O's (first player) and X's (second player) in the unoccupied cells of an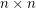 
grid. The first player (if any) to occupy a set of 
cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play?
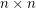grid. The first player (if any) to occupy a set of cells having no two cells in the same row or column is the winner. What is the outcome of the game given optimal play? Bibliography
* indicates original appearance(s) of problem.
Are there a simple solution?
On February 13th, 2013 Anonymous says:
I suspect, there are no simple answer and it can be solved only by heavy calculations, that is essentally there is no solution to this problem.
history and application
On February 22nd, 2013 mshj says:
i'm not sure but i think to solve this problem, i was wondering if any body gives me some information about the history and application of this problem
Drupal
CSI of Charles University
Solution
The problem has been solved. Link:- https://arxiv.org/abs/2101.00770