 login/create account
login/create account
57-regular Moore graph?
A Moore graph is a graph with diameter  and girth
and girth 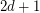 . It is known that every Moore graph is regular [S] (even distance-regular), and two (rather trivial) families of such graphs are provided by complete graphs and odd cycles. In one of the founding papers in the subject of algebraic graph theory, Hoffman and Singleton [HS] proved that every
. It is known that every Moore graph is regular [S] (even distance-regular), and two (rather trivial) families of such graphs are provided by complete graphs and odd cycles. In one of the founding papers in the subject of algebraic graph theory, Hoffman and Singleton [HS] proved that every  -regular Moore graph with diameter 2 must have
-regular Moore graph with diameter 2 must have 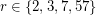 . For
. For 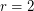 and
and 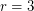 such graphs exist, are unique, and are familiar: the pentagon, and the Petersen graph. For
such graphs exist, are unique, and are familiar: the pentagon, and the Petersen graph. For 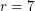 Hoffman and Singleton constructed such a graph - now known as the Hoffman-Singleton graph, but for
Hoffman and Singleton constructed such a graph - now known as the Hoffman-Singleton graph, but for 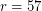 we are still uncertain whether such a graph exists.
we are still uncertain whether such a graph exists.
The pentagon, the Petersen graph, and the Hoffman-Singleton graph are all very highly symmetric graphs, and much of the interest in these objects is related to exceptional phenomena in small finite groups. In contrast to this, Higman proved that a 57-regular Moore graph cannot be vertex transitive (see [C]). In some sense, this is indication that even if a 57-regular Moore graph exists, it will be of less interest than its younger siblings. Nevertheless, as a lingering problem left by one of the first papers in algebraic graph theory, this is viewed as an important question.
There are some easily established properties of a 57-regular Moore graph. For instance it must have 3250 vertices and independence number at most 400. However it seems not nearly enough is known to narrow the search sufficiently.
Bibliography
[C] P. J. Cameron, Automorphisms of graphs in: Selected topics in graph theory, Volume 2, eds. L. W. Beineke and R. J. Wilson (Academic Press, London) 1983, pp. 89-127. MathSciNet
* [HS] A. J. Hoffman and R. R. Singleton, On Moore graphs with diameters 2 and 3. IBM J. Res. Develop. 4 (1960) 497--504. MathSciNet
[S] R. R. Singleton, There is no irregular Moore graph. American Mathematical Monthly 75, vol 1 (1968) 42–43. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University