 login/create account
login/create account
Let 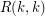 denote the
denote the 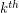 diagonal Ramsey number.
diagonal Ramsey number.
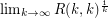 exists.
exists. Erdos offered $100 for a solution to the highlighted conjecture and $250 for a solution to the associated problem (these prizes are now provided by Graham).
Classic results of Erdos [E] and Erdos-Szekeres [ESz] give bounds on 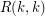 which show that if
which show that if 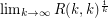 exists, then it is in the interval
exists, then it is in the interval ![$ [\sqrt{2},4] $](/files/tex/e60eefef54c8ed9f1796c217a67241a0e3ecd78e.png) . Although these arguments are quite basic, little progress has been made in improving these bounds. The best known lower bound on
. Although these arguments are quite basic, little progress has been made in improving these bounds. The best known lower bound on 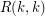 is due to Spencer [S] and the best known upper bound is due to Thomason [T]. They are as follows:
is due to Spencer [S] and the best known upper bound is due to Thomason [T]. They are as follows: 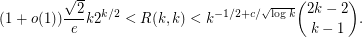
Gowers [G] has suggested that resolving these problems might require a rough structure theorem.
Bibliography
[E] P. Erdos, Some remarks on the theory of graphs, Bull. Amer. Math. Soc. 53 (1947), 292–294. MathSciNet
[ESz] P. Erdos and G. Szekeres, A combinatorial problem in geometry, Compositio Math. 2 (1935), 463–470.
[G] W. T. Gowers, Rough structure and classification, GAFA 2000 (Tel Aviv, 1999). Geom. Funct. Anal. 2000, Special Volume, Part I, 79--117. MathSciNet
[S] J. Spencer, Ramsey’s theorem—a new lower bound, J. Comb. Theory Ser. A 18 (1975), 108–115. MathSciNet
[T] A. Thomason, An upper bound for some Ramsey numbers, J. Graph Theory 12 (1988), 509–517. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University