A preprint by Jesper L. Jacobsen and Jesus Salas claims that there are graphs with roots of their flow polynomial being above 5. The generalized Petersen graphs G(7n,7) are claimed to have roots of flow polynomial that accumulate at approximately .
I suppose this makes the original conjecture truly false. An interesting variant, though, is to find out, if all roots of flow polynomials are . (Thanks to Bojan Mohar for pointing out the paper to me.)
Not bounded by 5, either
A preprint by Jesper L. Jacobsen and Jesus Salas claims that there are graphs with roots of their flow polynomial being above 5. The generalized Petersen graphs G(7n,7) are claimed to have roots of flow polynomial that accumulate at approximately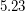 .
.
I suppose this makes the original conjecture truly false. An interesting variant, though, is to find out, if all roots of flow polynomials are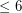 . (Thanks to Bojan Mohar for pointing out the paper to me.)
. (Thanks to Bojan Mohar for pointing out the paper to me.)