Open Problem Garden

Importance: Medium ✭✭

Author(s):

Subject:	Graph Theory
	» Coloring
	» » Nowhere-zero flows

Keywords:	flow polynomial
	nowhere-zero flow

Recomm. for undergrads: no

Posted	by:	mdevos
	on:	March 7th, 2007

Conjecture All real roots of nonzero flow polynomials are at most 4.

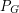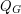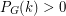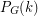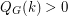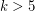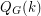For every graph $G$ , let $P_G$ be the chromatic polynomial of $G$ and let $Q_G$ be the flow polynomial of $G$ . If $G$ is loopless, then $P_G(k)>0$ for all sufficiently large integers $k$ (as $P_G(k)$ = # of k-colorings of $G$ ). It follows from Seymour's 6-flow theorem that if $G$ has no bridge, then $Q_G(k)>0$ for all integers $k>5$ (as $Q_G(k)$ = # of nowhere-zero flows in the group of integers modulo $k$ ). It is natural to ask if all real roots of these polynomials are small. 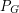For the chromatic polynomial, $P_G$ , this is not the case. There exist graphs with chromatic number 3 for which 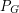$P_G$ has arbitrarily large real roots. The above conjecture asserts that the flow polynomial exhibits the opposite behavior. One word of caution, it is known that the set of roots of flow polynomials is dense in the complex plane.