 login/create account
login/create account
van der Waerden
Concavity of van der Waerden numbers ★★
Author(s): Landman
For 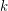 and
and 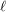 positive integers, the (mixed) van der Waerden number
positive integers, the (mixed) van der Waerden number 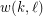 is the least positive integer
is the least positive integer  such that every (red-blue)-coloring of
such that every (red-blue)-coloring of ![$ [1,n] $](/files/tex/661d0acc09fbc5b62f49645a71cf7d831a26563f.png) admits either a
admits either a 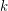 -term red arithmetic progression or an
-term red arithmetic progression or an 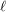 -term blue arithmetic progression.
-term blue arithmetic progression.
Conjecture For all 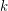 and
and 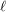 with
with 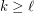 ,
, 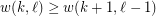 .
.
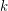 and
and 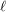 with
with 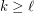 ,
, 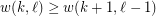 .
. Keywords: arithmetic progression; van der Waerden

 Drupal
Drupal CSI of Charles University
CSI of Charles University