 login/create account
login/create account
Simonovits, Miklos
Turán number of a finite family. ★★
Author(s): Erdos; Simonovits
Given a finite family 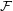 of graphs and an integer
of graphs and an integer  , the Turán number
, the Turán number 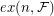 of
of 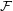 is the largest integer
is the largest integer  such that there exists a graph on
such that there exists a graph on  vertices with
vertices with  edges which contains no member of
edges which contains no member of 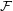 as a subgraph.
as a subgraph.
Conjecture For every finite family 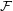 of graphs there exists an
of graphs there exists an 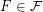 such that
such that 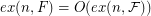 .
.
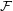 of graphs there exists an
of graphs there exists an 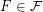 such that
such that 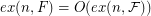 .
.
Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University