 login/create account
login/create account
satisfiability
Refuting random 3SAT-instances on $O(n)$ clauses (weak form) ★★★
Author(s): Feige
Conjecture For every rational 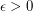 and every rational
and every rational  , there is no polynomial-time algorithm for the following problem.
, there is no polynomial-time algorithm for the following problem.
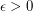 and every rational
and every rational  , there is no polynomial-time algorithm for the following problem.
, there is no polynomial-time algorithm for the following problem.
Given is a 3SAT (3CNF) formula 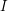 on
on  variables, for some
variables, for some  , and
, and 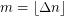 clauses drawn uniformly at random from the set of formulas on
clauses drawn uniformly at random from the set of formulas on  variables. Return with probability at least 0.5 (over the instances) that
variables. Return with probability at least 0.5 (over the instances) that 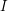 is typical without returning typical for any instance with at least
is typical without returning typical for any instance with at least 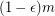 simultaneously satisfiable clauses.
simultaneously satisfiable clauses.
Keywords: NP; randomness in TCS; satisfiability

 Drupal
Drupal CSI of Charles University
CSI of Charles University