 login/create account
login/create account
planar
Degenerate colorings of planar graphs ★★★
Author(s): Borodin
A graph  is
is  -degenerate if every subgraph of
-degenerate if every subgraph of  has a vertex of degree
has a vertex of degree 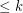 .
.
Conjecture Every simple planar graph has a 5-coloring so that for 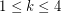 , the union of any
, the union of any  color classes induces a
color classes induces a 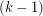 -degenerate graph.
-degenerate graph.
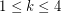 , the union of any
, the union of any  color classes induces a
color classes induces a 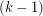 -degenerate graph.
-degenerate graph. Keywords: coloring; degenerate; planar
The Two Color Conjecture ★★
Author(s): Neumann-Lara
Conjecture If  is an orientation of a simple planar graph, then there is a partition of
is an orientation of a simple planar graph, then there is a partition of 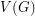 into
into 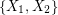 so that the graph induced by
so that the graph induced by 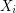 is acyclic for
is acyclic for 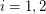 .
.
 is an orientation of a simple planar graph, then there is a partition of
is an orientation of a simple planar graph, then there is a partition of 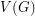 into
into 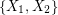 so that the graph induced by
so that the graph induced by 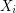 is acyclic for
is acyclic for 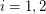 .
. 
 Drupal
Drupal CSI of Charles University
CSI of Charles University