 login/create account
login/create account
Ossona de Mendez, Patrice
Linear Hypergraphs with Dimension 3 ★★
Author(s): de Fraysseix; Ossona de Mendez; Rosenstiehl
Conjecture Any linear hypergraph with incidence poset of dimension at most 3 is the intersection hypergraph of a family of triangles and segments in the plane.
Keywords: Hypergraphs
Straight line representation of planar linear hypergraphs ★★
Author(s): de Fraysseix; Ossona de Mendez
Conjecture Every planar linear hypergraph 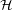 has a straight line representation in the plane which maps each vertex
has a straight line representation in the plane which maps each vertex  to a point
to a point 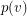 and each edge
and each edge  to a straight line segment
to a straight line segment 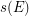 , in such a way that:
, in such a way that:
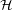 has a straight line representation in the plane which maps each vertex
has a straight line representation in the plane which maps each vertex  to a point
to a point 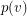 and each edge
and each edge  to a straight line segment
to a straight line segment 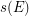 , in such a way that:
, in such a way that:- \item for each vertex
 and each edge
and each edge  , we have:
, we have: 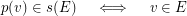 \item for each couple of distinct edges
\item for each couple of distinct edges 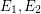 , we have
, we have 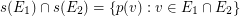
Keywords: intersection graph; planar hypergraph

 Drupal
Drupal CSI of Charles University
CSI of Charles University