 login/create account
login/create account
elliptic
Quartic rationally derived polynomials ★★★
Author(s): Buchholz; MacDougall
Call a polynomial ![$ p \in {\mathbb Q}[x] $](/files/tex/a72fcb0a006c3c2afb3ba69722ccdb2599b83e90.png) rationally derived if all roots of
rationally derived if all roots of 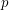 and the nonzero derivatives of
and the nonzero derivatives of 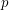 are rational.
are rational.
Conjecture There does not exist a quartic rationally derived polynomial ![$ p \in {\mathbb Q}[x] $](/files/tex/a72fcb0a006c3c2afb3ba69722ccdb2599b83e90.png) with four distinct roots.
with four distinct roots.
![$ p \in {\mathbb Q}[x] $](/files/tex/a72fcb0a006c3c2afb3ba69722ccdb2599b83e90.png) with four distinct roots.
with four distinct roots. Keywords: derivative; diophantine; elliptic; polynomial

 Drupal
Drupal CSI of Charles University
CSI of Charles University