Home » Subject » Graph Theory

Star chromatic index of cubic graphs

Importance: Medium ✭✭
Author(s): Dvorak, Zdenek
Mohar, Bojan
Samal, Robert
Subject: Graph Theory
Keywords: edge coloring
star coloring
Recomm. for undergrads: no
Posted by: Robert Samal
on: November 16th, 2010

The star chromatic index 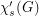$ \chi_s'(G) $ of a graph $ G $ is the minimum number of colors needed to properly color the edges of the graph so that no path or cycle of length four is bi-colored.

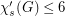Question   Is it true that for every (sub)cubic graph $ G $, we have $ \chi_s'(G) \le 6 $?

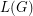The star chromatic number is the more usual concept [ACKKR,FRR]. Star chromatic index of a graph $ G $ is simply the star chromatic number of the line graph $ L(G) $; the definition given above is easily seen to be equivalent.

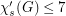Dvořák, Mohar, and Šámal [DMS] show that every (sub)cubic graph $ G $, satisfies $ \chi_s'(G) \le 7 $? On the other hand, it is simple to check that $ \chi_s'(K_{3,3])=6 $, so the conjecture, if true, is tight.

Bibliography

[ACKKR] Albertson, Michael O.; Chappell, Glenn G.; Kierstead, Hal A.; Kündgen, André; Ramamurthi, Radhika: Coloring with no 2-Colored P4's, The Electronic Journal of Combinatorics 11 (1).

[FRR] Fertin, Guillaume; Raspaud, André; Reed, Bruce, Star coloring of graphs, Journal of Graph Theory 47 (3): 163-182, doi:10.1002/jgt.20029 .

*[DMS] Dvořák, Zdeněk; Mohar, Bojan; Šámal, Robert: Star chromatic index, arXiv:1011.3376.


* indicates original appearance(s) of problem.
add new comment