 login/create account
login/create account
Lindelöf hypothesis
Conjecture For any 
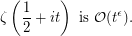

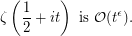
Since  can be replaced by a smaller value, we can also write the conjecture as, for any positive
can be replaced by a smaller value, we can also write the conjecture as, for any positive  ,
, 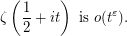
Lindelof hypothesis in Wikipedia.
Accordingly Wikipedia this hypothesis is implied by Riemann hypothesis.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University