 login/create account
login/create account
Imbalance conjecture
Conjecture Suppose that for all edges 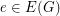 we have
we have 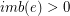 . Then
. Then 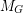 is graphic.
is graphic.
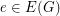 we have
we have 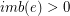 . Then
. Then  is graphic.
is graphic. Consider simple undirected graph  and let
and let 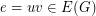 .
.
The imbalance of the edge  defined as
defined as 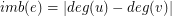 .
.
The multiset of all edge imbalances of  is denoted by
is denoted by 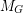 .
.
Note, that conjecture is verified for all such graphs with 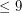 vertices.
vertices.
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University