 login/create account
login/create account
Growth of finitely presented groups
See Wikipedia's growth of groups for definitions of the basics reguarding growth rate in groups (in particular polynomial and exponential growth rates). A finitely generated group has intermediate growth if its growth rate (for every finite generating set) is subexponential but superpolynomial.
Most naturally occuring groups have either polynomial growth (such as 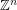 ) or exponential growth (such as a free group with rank
) or exponential growth (such as a free group with rank 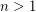 ). Milnor [M] famously asked if there exists a finitely generated group with intermediate growth, and this problem was resolved in the affirmative by Grigorchuk [G]. The groups constructed by Grigorchuk are not finitely presented, thus leaving the above problem.
). Milnor [M] famously asked if there exists a finitely generated group with intermediate growth, and this problem was resolved in the affirmative by Grigorchuk [G]. The groups constructed by Grigorchuk are not finitely presented, thus leaving the above problem.
Expert opinion seems to be that there are no finitely presented groups of intermediate growth.
Bibliography
[G] R. I. Grigorchuk, Degrees of growth of finitely generated groups and the theory of invariant means., Izv. Akad. Nauk SSSR Ser. Mat. 48:5 (1984), 939-985.
[M] J. Milnor, A note on curvature and fundamental group, J. Differential Geometry 2 (1968), 1-7.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University