 login/create account
login/create account
| Recomm. for undergrads: no |
| Posted | by: | princeps |
| on: | March 27th, 2012 |
 is a prime iff
is a prime iff 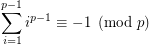
[BBBG] Borwein, D.; Borwein, J. M., Borwein, P. B., and Girgensohn, R. "Giuga's Conjecture on Primality", American Mathematical Monthly, 103, 40–50, (1996)