Open Problem Garden

The Riemann zeta serie is the function of the complex variable defined by 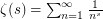. It is defined only for a real part of greater than 1. It is an analytic function on this domain, and there exists a unique analytic function defined over the whole complex plane (except at 1) that coincides with zeta when 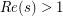. This function is the analytic continuation of the Riemann zeta serie, and is called the Riemann zeta function, on which is based the Riemann Hypothesis. It was stated by Bernhard Riemann in 1859 and is still open. The zeta function and the Riemann Hypothesis are closely related to number theory and the distribution of prime numbers, as is well described in wikipedia. For that reason this item could also lie under the "Number Theory" category of this website.

A lot of variants and extensions of the Riemann hypothesis have been raised till today. The location on the Critical line of the so-called "non trivial zeroes" of zeta (the ones in the Critical Strip, by opposition to the trivial ones that are negative even integers and are well known) is supposed to be also valid for the analytic continuation of Dirichlet L-series associated to a primitive Dirichlet character 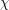: 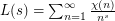. It is also believed to be valid for Dedekind zeta functions (generalization of zeta related to number fields, that is a finite dimensional extension of the field of rational numbers), also for Hecke L-functions associated to Hecke Grossencharacters (generalization to number fields of the Dirichlet L-functions), for Artin L-functions etc... The list of various generalizations is now long. Today, the largest class of functions that are expected to obey a Riemann Hypothesis are functions in the Selberg Class, even though zeta functions for motives over schemes are also candidates.

There exists a few variants of the Riemann Hypothesis for which the hypothesis is now solved: For the zeta functions of elliptic curves over finite fields, the problem was solved by André Weil (1950). For zeta functions associated to local fields it has been proved by Daniel Bump, Eugene Ng, Jeffrey Vaaler, Stephen Choi, Par Kurlberg [B] in the real Case (= the Mellin transform of the hermite functions behave like zeta), by Par Kurlberg in the non-archimedean case with odd residue characteristics and recently par Oloffson (2006) in the complex case even though it was previously believed it was wrong in that case. It is remarkable that the local (archimedean) results also apply to the Mellin transform of the laguerre functions, thanks to the properties of the second order differential equation fulfilled by the Laguerre functions. It supports (if necessary) the link between this problem and Harmonic Analysis (see also publications by Davidson, Olafson, Faraut [F] etc on representations of conformal groups underlying Jordan algebras on bounded symmetric domains). Polya [P] succeeded around 1926 to proove that some approximations of zeta do actually have their zeroes on the Critical Line, However his results cannot be directly generalized to zeta itself (see [T]). But there are actually a lot of ways to explore the Riemann Hypothesis, from pure Number Theory to Random Matrices or Non-Commutative Geometry, which makes this problem one of the most difficult mathematical problem today.

The zeta function is also amazing, since it is the first explicit function discovered to be "Universal" (in the sense that any analytic function that does not vanish in a small disk can be uniformly approximated by zeta up to a suitable translation of zeta in the complex plane). This result was proved in 1975 by Voronin, and Karatsuba generalized the result to a finite set of L-functions approximating a finite set of analytic functions. Before this discovery, the existence of a universal function was proven in the 50's by a construction requiring the use of the axiom of choice. This result has an impact in the context of the Riemann hypothesis, because it shows that any linear combination of some Dirichlet L-functions (with non-vanishing coefficients) do not follow the Riemann Hypothesis (such a linear combination actually vanishes infinitely many times in any vertical strip inside the Critical Strip). This result is even more important when specializing to a special kind of linear combinations of Dirichlet L-functions, the prototype of which is the Davenport Heilbronn L-function. This specific linear combination share a symmetry property with individual Dirichlet L-functions (a symmetry by the change of variable 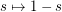) which is expressed by the so-called "functional equation" fulfilled by zeta as well as Dirichlet L-functions, Hecke L-functions etc.. This functional equation is very important in this problem since in the specific case of zeta it exactly characterizes the zeta function, and with additional conditions it characterizes also Dirichlet L-functions (these are the so-called "Converse theorems", the first of which was proven by Hans Hamburger [H]). The example of the Davenport Heilbronn L-functions shows that the exact form of the functional equation is essential in the context of the Riemann Hypothesis (the functional equation of the Davenport Heilbronn L-function is almost the same as the one of a single Dirichlet L-function but there is a slight difference). However, the functional equation 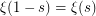where 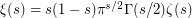(and similarly for L-functions), is far from beeing sufficient to prove that the non trivial zeroes are located on the Critical Line, and it is widely agreed that the missing information will require to imagine new mathematical concepts.

See also the article of Peter Sarnak on the Clay Institute website, as well as the link about the Millenium Prize.

E.C.