login/create account
Consider a set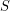 
of great circles on a sphere with no three circles meeting at a point. The arrangement graph of 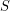has a vertex for each intersection point, and an edge for each arc directly connecting two intersection points. So this arrangement graph is 4-regular and planar.
Conjecture Every arrangement graph of a set of great circles is 
-colourable.
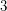-colourable. It is NP-complete to test 3-colourability of planar 4-regular graphs in general [D80].
Arrangement graphs of general circles on the sphere can require four colors [K90].
A stronger conjecture states that the arrangement graph of every set of great circles is 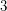-choosable. A natural approach is to use the machinery of [AT92].
Previously appeared here.
Bibliography
[AT92] Noga Alon and Michael Tarsi. Colourings and orientations of graphs. Combinatorica 12:125--134, 1992.
*[FHNS00] Stefan Felsner, Ferran Hurtado, Marc Noy, and Ileana Streinu. Hamiltonicity and colorings of arrangement graphs. In Proc. 11th Annual ACM-SIAM Symp. Discrete Algorithms (SODA), pages 155--164, January 2000.
[FHNS06] Felsner, Stefan; Hurtado, Ferran; Noy, Marc; Streinu, Ileana. Hamiltonicity and colorings of arrangement graphs. Discrete Appl. Math. 154 (2006), no. 17, 2470--2483.
[K90] G. Koester. 4-critical, 4-valent planar graphs constructed with crowns. Math. Scand., 67:15--22, 1990.
[D80] D. P. Dailey. Uniqueness of colorability and colorability of planar 4-regular graphs are NP-complete, Discrete Math. 30:289--193, 2980.
* indicates original appearance(s) of problem.
Drupal
CSI of Charles University