 login/create account
login/create account
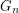 be the bipartite graph whose vertices are the
be the bipartite graph whose vertices are the  -subsets and the
-subsets and the 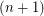 -subsets of a
-subsets of a 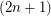 -element set, and with inclusion as the adjacency relationship. Then
-element set, and with inclusion as the adjacency relationship. Then 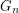 is Hamiltonian.
is Hamiltonian.
The graph 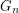 is known as the middle-levels graph because it may be thought of as the graph formed by the cover relations between the middle two layers of the Hasse diagram of the Boolean lattice of all subsets of a
is known as the middle-levels graph because it may be thought of as the graph formed by the cover relations between the middle two layers of the Hasse diagram of the Boolean lattice of all subsets of a 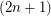 -element set, partially ordered by inclusion. The conjecture has been computationally verified up to
-element set, partially ordered by inclusion. The conjecture has been computationally verified up to 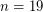 [AS] (Announced only at end of paper). It is also known that
[AS] (Announced only at end of paper). It is also known that 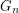 contains a cycle containing at least
contains a cycle containing at least 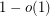 of its vertices [J] and that
of its vertices [J] and that 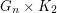 is Hamiltonian [HKRR].
is Hamiltonian [HKRR].
Bibliography
[HKRR] Peter Horák, Tomáš Kaiser, Moshe Rosenfeld, Zdeněk Ryjáček, The prism over the middle-levels graph is Hamiltonian, Order 22 (2005), no. 1, 73--81.
[J] Robert J. Johnson, Long cycles in the middle two layers of the discrete cube. J. Combin. Theory Ser. A 105 (2004), no. 2, 255--271. MathSciNet
[SW] Carla D. Savage and Peter Winkler, Monotone Gray codes and the middle levels problem, J. Combin. Theory Ser. A 70 (1995), no. 2, 230--248.
[SSS] Ian Shields, Brendan J. Shields, Carla D. Savage, An update on the middle levels problem, preprint.
[AS] Kazuyuki Amano, Manabu Shimada, A Note on the Middle Levels Conjecture, preprint.
[M] Mütze, Torsten. “Proof of the Middle Levels Conjecture.” Proceedings of the London Mathematical Society. Third Series 112, no. 4 (2016): 677–713.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University