Home » Subject » Graph Theory » Coloring » Nowhere-zero flows
Importance: High ✭✭✭
Author(s): Goddyn, Luis A.
Seymour, Paul D.
Subject: Graph Theory
» Coloring
» » Nowhere-zero flows
Keywords: edge-connectivity
flow
Recomm. for undergrads: no
Prize: none
Posted by: mdevos
on: March 7th, 2007
Solved by: L. M. Lovász, C. Thomassen, Y. Wu, and C.-Q. Zhang. Nowhere-zero 3-flows and modulo k-orientations. J. Combin. Theory Ser. B, 103(5):587–598, 2013.
Conjecture   For every $ \epsilon>0 $ there exists an integer $ k $ so that every $ k $-edge-connected graph has a $ (2+\epsilon) $-flow.

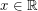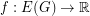Definition: If $ G $ is a directed graph and $ x \in {\mathbb R} $, a real $ x $-flow (sometimes abbreviated $ x $-flow) of $ G $ is a real valued flow $ f:E(G)\to {\mathbb R} $ with the property that 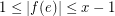$ 1 \le |f(e)| \le x-1 $ for every $ e \in E(G) $. As in the case of nowhere-zero flows, the existence of an $ x $-flow in a graph does not depend on the orientation, and we say that an undirected graph has an $ x $-flow if some (and thus every) orientation of it admits such a flow. 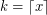It is a simple exercise to prove that every graph with a real $ x $-flow has an (integer) nowhere-zero $ k $-flow where $ k = \lceil x \rceil $. Thus, we may view $ x $-flows as a refinement of nowhere-zero $ k $-flows.

This conjecture has a strong intuitive appeal. Simply put, the above conjecture asserts that in a graph with high edge-connectivity, it is possible to find a real-valued flow where every edge has about the same flow value. By the above comment relating $ x $-flows and nowhere-zero $ k $-flows, this conjecture (if true) would imply The weak 3-flow conjecture (See 3-flow conjecture). Zhang [Z] has proved that this result holds when restricted to graphs on a fixed surface, but little else seems to be known.

L. M. Lovász, C. Thomassen, Y. Wu, and C.-Q. Zhang solved this conjecture by proving the following.

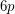For every positive integer $ p $, every $ 6p $-edge-conneected graph admits a nowhere-zero circular 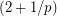$ (2+1/p) $-flow.

Bibliography

[KZ] W. Klostermeyer and C. Q. Zhang, 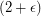$ (2+\epsilon) $-coloring of planar graphs with large odd-girth. Graph Theory 33 (2000), no. 2, 109--119. MathSciNet

[Z] C. Q. Zhang, Cun Quan, Circular flows of nearly Eulerian graphs and vertex-splitting. J. Graph Theory 40 (2002), no. 3, 147--161. MathSciNet

[LTWZ] L. M. Lovász, C. Thomassen, Y. Wu, and C.-Q. Zhang. Nowhere-zero 3-flows and modulo k-orientations. J. Combin. Theory Ser. B, 103(5):587–598, 2013.


* indicates original appearance(s) of problem.
1 comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options