 login/create account
login/create account
planar graph
Bounded colorings for planar graphs ★★
Author(s): Alon; Ding; Oporowski; Vertigan
Question Does there exists a fixed function 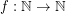 so that every planar graph of maximum degree
so that every planar graph of maximum degree  has a partition of its vertex set into at most three sets
has a partition of its vertex set into at most three sets 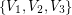 so that for
so that for 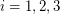 , every component of the graph induced by
, every component of the graph induced by 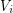 has size at most
has size at most 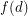 ?
?
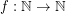 so that every planar graph of maximum degree
so that every planar graph of maximum degree  has a partition of its vertex set into at most three sets
has a partition of its vertex set into at most three sets 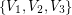 so that for
so that for 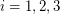 , every component of the graph induced by
, every component of the graph induced by 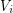 has size at most
has size at most 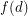 ?
? Keywords: coloring; partition; planar graph
Universal point sets for planar graphs ★★★
Author(s): Mohar
We say that a set 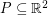 is
is  -universal if every
-universal if every  vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in
vertex planar graph can be drawn in the plane so that each vertex maps to a distinct point in  , and all edges are (non-intersecting) straight line segments.
, and all edges are (non-intersecting) straight line segments.
Question Does there exist an  -universal set of size
-universal set of size 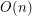 ?
?
 -universal set of size
-universal set of size 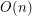 ?
? Keywords: geometric graph; planar graph; universal set
What is the largest graph of positive curvature? ★
Problem What is the largest connected planar graph of minimum degree 3 which has everywhere positive combinatorial curvature, but is not a prism or antiprism?
Keywords: curvature; planar graph

 Drupal
Drupal CSI of Charles University
CSI of Charles University