Home » Subject » Graph Theory » Coloring » Vertex coloring

Are vertex minor closed classes chi-bounded?

Importance: Medium ✭✭
Author(s): Geelen, Jim
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords: chi-bounded
circle graph
coloring
vertex minor
Recomm. for undergrads: no
Posted by: mdevos
on: May 16th, 2009
Question   Is every proper vertex-minor closed class of graphs chi-bounded?

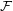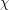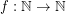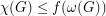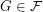We say that a family of graphs $ {\mathcal F} $ is $ \chi $-bounded if there is a function $ f : {\mathbb N} \rightarrow {\mathbb N} $ so that $ \chi(G) \le f( \omega(G)) $ for every $ G \in {\mathcal F} $.

If $ G $ is a simple graph, a vertex minor of $ G $ is any graph which can be obtained by a sequence of the following operations:

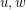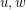    \item delete a vertex \item choose a vertex $ v $ and complement the neighborhood of $ v $ (i.e. whenever $ u,w $ are neighbors of $ v $, switch $ u,w $ between adjacent/non-adjacent).

Dvorak and Kral [DK] showed that this conjecture is true for class of graphs of bounded rank-width, and the class of graphs having no vertex-minor isomorphic to the wheel 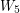$ W_5 $ on $ 6 $ vertices.

Bibliography

[DK] Z. Dvorak and D. Král. Classes of graphs with small rank decompositions are χ-bounded. European J. Combin., 33(4):679–-683, 2012. MathSciNet


* indicates original appearance(s) of problem.
add new comment